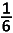 n(n − 1)(3n2 − n − 1)
n(n − 1)(3n2 − n − 1)Met SPOn bedoelen we de som van alle mogelijke producten,
twee aan twee, van de eerste n oneven getallen
Bijvoorbeeld : voor {1, 3, 5, 7} is
SPO4 = 3 + 5+ 7+ 15 + 21 + 35 = 86
LL = 1.3 = 3
RL =
LL = RL → O.K.
| Te bewijzen : | SPOn = 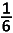 n(n − 1)(3n2 − n − 1) n(n − 1)(3n2 − n − 1)Met SPOn bedoelen we de som van alle mogelijke producten, twee aan twee, van de eerste n oneven getallen Bijvoorbeeld : voor {1, 3, 5, 7} is SPO4 = 3 + 5+ 7+ 15 + 21 + 35 = 86 | |
| Bewijs : | ||
| Deel I : |
Voor de kleinste n-waarde, nl. 2 is LL = 1.3 = 3 RL = LL = RL → O.K. |
| Deel II : | Gegeven : |
SPOk = 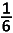 k(k − 1)(3k2 − k − 1) k(k − 1)(3k2 − k − 1)
|
| Te bewijzen : |
SPOk+1 = 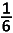 (k+1).k.(3k2 + 5k + 1) (k+1).k.(3k2 + 5k + 1)3(k+1)²−(k+1)−1 = 3k²+6k+3−k−1−1 = 3k²+5k+1 | |
| Bewijs : | SPOk+1 = SPOk + [2(k+1) − 1][1 + 3 + ... + (2k−1)] (k termen) | |
__
= 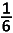 k(k − 1)(3k2 − k − 1) + (2k + 1). k(k − 1)(3k2 − k − 1) + (2k + 1). .k.(1 + 2k−1) .k.(1 + 2k−1)
| ||
__
= 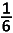 k [(k − 1)(3k2− k − 1) + 6 k (2k + 1)] k [(k − 1)(3k2− k − 1) + 6 k (2k + 1)]
| ||
__
= 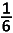 k (3k3 − k2 − k − 3k2 + k + 1 + 12k2 + 6k) k (3k3 − k2 − k − 3k2 + k + 1 + 12k2 + 6k)
| ||
__
= 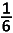 k (3k3 + 8k2 + 6k + 1) V(−1) = −3+8− 6+1 = 0 + HORNER k (3k3 + 8k2 + 6k + 1) V(−1) = −3+8− 6+1 = 0 + HORNER
| ||
__
= 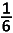 k (k + 1)(3k2 + 5k + 1) k (k + 1)(3k2 + 5k + 1)
| ||
| __ = RL Q.E.D. |